
Matlab Code for Haze Removal
₹3,000.00
Huge Price Drop : 50% Discount
Source Code + Demo Video
100 in stock
Description
HAZE REMOVAL

Figure: Haze removal result. (a) Input haze image. (b) Estimated transmission map. (c) Refined transmission map after soft matting. (d) Final haze-free image.
Images of outdoor scenes are usually degraded by the turbid medium (e.g., particles, water-droplets) in the atmosphere. Haze, fog, and smoke are such phenomena due to atmospheric absorption and scattering. The irradiance received by the camera from the scene point is attenuated along the line of sight. Furthermore, the incoming light is blended with the airlight (ambient light reflected into the line of sight by atmospheric particles). The degraded images lose the contrast and color fidelity . Since the amount of scattering depends on the distances of the scene points from the camera, the degradation is spatial-variant.
Haze removal (or dehazing) is highly desired in both consumer/computational photography and computer vision applications. First, removing haze can significantly increase the visibility of the scene and correct the color shift caused by the airlight. In general, the haze-free image is more visually pleasuring. Second, most computer vision algorithms, from low-level image analysis to high-level object recognition, usually assume that the input image (after radiometric calibration) is the scene radiance. The performance of vision algorithms (e.g., feature detection, filtering, and photometric analysis) will inevitably suffers from the biased, low-contrast scene radiance. Last, the haze removal can produce depth information and benefit many vision algorithms and advanced image editing. Haze or fog can be a useful depth clue for scene understanding. The bad haze image can be put to good use.
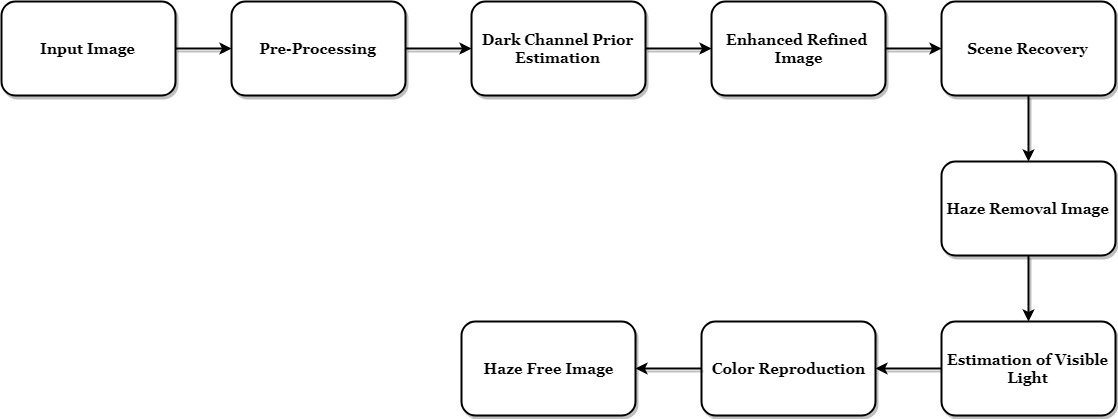
Images captured during adverse weather conditions frequently feature degraded visibility and undesirable color cast effects. Images captured in foggy weather conditions often suffer from poor visibility, which will create a lot of impacts on the outdoor computer vision systems, such as video surveillance, intelligent transportation assistance system, and remote sensing space cameras and so on. One of the central problems in image processing in open-air is the presence of cloud, fog or smoke which fades the colors and reduces the contrast of the observed things. Images of outdoor scenes captured during inclement weather conditions. Image processing techniques improve the quality of an image and enhance the maximum information from the degraded image. In this paper, we propose a effective Dark Channel Prior technique, which is apply on selected region to estimate the atmospheric light, and obtain more accurate result. The Dark Channel Prior is a kind of statistics of the haze-free outdoor image. And thus it obtains a high-quality haze-free image using Image processing approach.
INTRODUCTION
Bad weather conditions such as haziness, mist, foggy and smoky degradation in the quality of the outdoor scene. It is an annoying problem to photographers as it changes the colors and reduces the contrast of daily photos, it diminishes the visibility of the scenes and it is a threat to the reliability of many applications like outdoor surveillance, object detection, it also decreases the clarity of the satellite images and underwater images. So removing haze from images is an imperative and broadly demanded area in image processing. The large quantities of these suspended particles in atmosphere cause scattering of light before it reaches the camera which corrupts the outdoor image quality. Haze attenuates the reflected light from the scenes and blends it with additive light in atmosphere. Haze removal techniques tend to improve this reflected light (i.e. scene colors) from mixed light. The constancy and strength of the visual system can also be improved by using this effective haze removal of image. There are many methods available to remove haze from image like polarization independent component analysis, dark channel prior etc.
EXISTING SYSTEM
The visibility restoration approach using Laplacian-method to remove fog thickness estimation and color cast problems
PROPOSED METHOD
Algorithm to refine the different kinds of an amorphous on the foggy image after apply dark channel prior. The results showed that this method makes the dehazing result more close to actual scene. The procedure is developed mainly for enhancing images acquired under extremely low light situation where the features of images are nearly unseen. After using better and effective image defog algorithm to the inverted input image, the contrast get improved and the dark surface become bright when the intensity can be amplified.
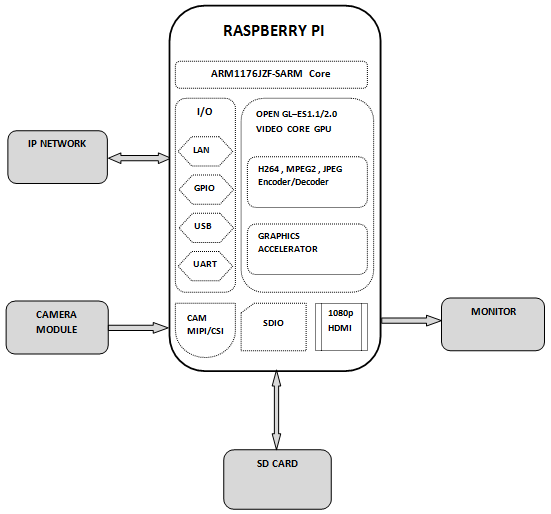
BLOCK DIAGRAM
ADVANTAGES
- It avoids halo effect and insufficient transmission estimation problems.
- It recovers better image quality under various weather condition changes.
- Less algorithm complexity.
- Its processing time is low.
APPLICATIONS
- Advanced Driver Assistance System
- Video Surveillance systems
- Obstacle Detection systems
- Outdoor Object recognition systems
SOFTWARE REQUIREMENTS
- MATLAB 7.14 or above versions
CONCLUSION
Haze removal algorithms have become a need for various computer vision based applications. But in already existing approaches, many aspects have been neglected i.e. No technique is accurate in different situation. Survey has displayed the neglected points in the presented methods like the noise reduction methods. The problem of uneven and over illumination is also an issue for dehazing methods. So there is a need of modification in the existing methods so that existing methods work in better way
REFERENCES
[1] Tan, Robby T, “Visibility in bad weather from a single image” IEEE Conference on Computer Vision and Pattern Recognition, CVPR, pp. 1-8, Year 2008.
[2] Tarel, J-P. and Nicolas Hautiere, “Fast visibility restoration from a single color or gray level image”, 12th International Conference on Computer Vision, pp. 2201-2208, Year 2009.
[3] Yu, Jing, Chuangbai Xiao and Dapeng Li, “Physics-based fast single image fog removal.”,10th IEEE International Conference on Signal Processing (ICSP), pp. 1048-1052, Year 2010.
[4] Fang, Faming, Fang Li, Xiaomei Yang, Chaomin Shen and Guixu Zhang, “Single image dehazing and denoising with variational method”, IEEE International Conference on Image Analysis and Signal Processing (IASP), pp. 219-222, 2010.
[5] He, Kaiming, Jian Sun and Xiaoou Tang, “Single image haze removal using dark channel prior.”,IEEE Transactions on Pattern Analysis and Machine Intelligence, vol.33, no. 12, pp. 2341- 2353,2011.
[6] Long, Jiao, Zhenwei Shi and Wei Tang, “Fast haze removal for a single remote sensing image using dark channel prior”, International Conference on Computer Vision in Remote Sensing (CVRS), pp.132-135, 2012.
[7] Zhang, Yong-Qin, Yu Ding, Jin-Sheng Xiao, Jiaying Liu and Zongming Guo, “Visibility enhancement using an image filtering approach”, EURASIP Journal on Advances in Signal Processing, no. 1, pp. 1-6, 2012.
[8] Xu, Haoran, Jianming Guo, Qing Liu and Lingli Ye, “Fast image dehazing using improved dark channel prior”, IEEE International Conference on Information Science and Technology (ICIST), pp. 663-667, 2012

Reviews
There are no reviews yet.