Lifting based Discrete Wavelet Transform using Spartan3 FPGA Image Processing Kit
Call for Price
In this project, we implement algorithms for efficient implementation of lifting based Discrete Wavelet Transform (DWT) using Spartan3 FPGA Image Processing Kit.
Features:
IMAGE PROCESSING APPLICATIONS USING FPGA
Shipping : 2 to 3 working days from the Date of purchase
Package Includes:
-
Complete Hardware Kit
-
Demo Video-Embedded Below
-
Abstract
-
Reference Paper
-
!!! Online Support !!!
Description
Abstract
In this project, we implement algorithms for efficient implementation of lifting based Discrete Wavelet Transform (DWT) using Spartan3 FPGA Image Processing Kit. The basic principle behind the lifting based scheme is to decompose the finite impulse response (FIR) filters in wavelet transform into a finite sequence of simple filtering steps. Lifting based DWT implementations have many advantages, and have recently been proposed for the JPEG2000 standard for image compression. Consequently, this has become an area of active research and several architectures have been proposed in recent years. In this paper, we provide a survey of these architectures for both 1-dimensional and 2-dimensional DWT. The architectures are representative of many design styles and range from highly parallel architectures to DSP-based architectures to folded architectures. We provide a systematic derivation of these architectures along with an analysis of their hardware and timing complexities.
Demonstration Video
Tool required
Software:
- Xilinx ISE 10.1i or above
- Xilinx EDK 10.1i or above
- VB GUI to display output
Language:
- VHDL, System C
Hardware:
- Spartan3 FPGA Image Processing Kit
- JTAG Cable
- PC
- Serial Cable
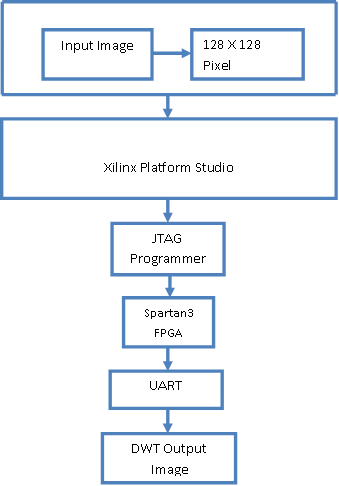
Block Diagram for Lifting based Discrete Wavelet Transform
Introduction:
Fusion steps based on wavelet transform can be summarized
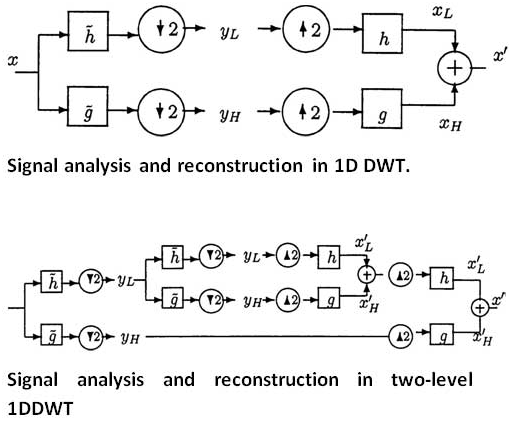
In traditional convolution (filtering) based approach for computation of the forward DWT, the input signal (x) is filtered separately by a low-pass filter (h˜) and a high-pass filter (g˜). The two output streams are then sub-sampled by simply dropping the alternate output samples in each stream to produce the low-pass (yL) and high-pass (yH) subband outputs as shown in Fig. 1. The two filters (h”, g”) form the analysis filter bank. The original signal can be reconstructed by a synthesis filter bank (h, g) starting from yL and yH as shown in Fig. 1. Given a discrete signal x(n), the output signals yL(n) and yH(n) in Fig. 1 can be computed as follows:
where tL and tH are the lengths of the low-pass (“h) and high-pass ( “g) filters respectively. During the inverse transform computation, both yL and yH are first up- sampled by inserting zeros in between two samples and then filtered by
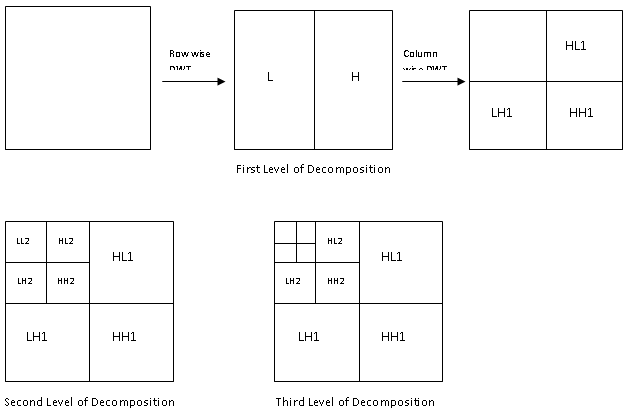
sampled by inserting zeros in between two samples and then filtered by low-pass (h) and high-pass (g) filters respectively. Then they are added together to obtain the reconstructed signal (x_) as shown in Fig. 1. For multiresolution wavelet decomposition, the lowpass subband (yL) is further decomposed in a similar fashion in order to get the second-level of decomposition, and the process repeated. The inverse process follows similar multi-level synthesis filtering in order to reconstruct the signal. A two level DWT decomposition and its reconstruction have been shown in Fig. 2, as an example. Since two dimensional wavelet filters are separable functions, 2D DWT can be obtianed by first applying the 1D DWT row-wise (to produce L and H subbands in each row) and then column-wise as shown in Fig. 3(a). In the first level of decomposition, four subbands LL1, LH1, HL1 and HH1 are obtained. Repeating the same in the LL1 subband, it produces LL2, LH2, HL2 and HH2 and so on, as shown in Fig. 3(c).
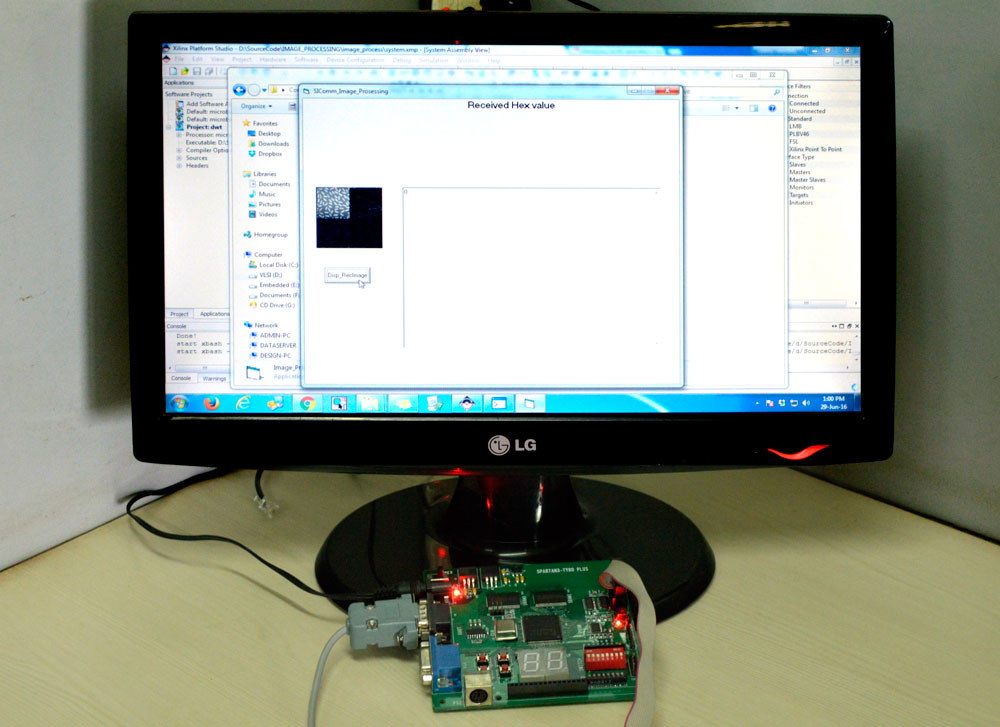
Output Image
Lifting Based Discrete Output Image
Conclusion
In this project, we implemented lifting based implementations of 2-dimensional Discrete Wavelet Transform using Spartan3 FPGA Image Processing Kit. We briefly described the principles behind the lifting scheme in order to better understand the different implementation styles and structures. We have presented several architectures of different flavors ranging from highly parallel ones to highly folded ones to programmable ones. We provided a systematic derivation of each architecture and evaluated them with respect to their hardware and timing requirements.
Additional information
| Weight | 1.000000 kg |
|---|



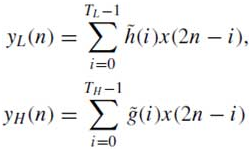










Reviews
There are no reviews yet.