Matlab Code for Integer Wavelet Transform
₹3,000.00
Huge Price Drop : 50% Discount
Source Code + Demo Video
100 in stock
Description
Human visual system (HVS) is less sensitive to the high resolution detail bands like HL, LH and HH. Wavelet domain hides data in these regions. Hiding data in the high resolution regions increases the robustness while maintaining good visual quality. In discrete wavelet transform, the wavelet filters have floating point coefficients. When the data is hided in their coefficients, any truncations of the floating point values of the pixels that should be integers may cause the loss of the hidden information. It may lead to the failure of the data hiding system .
DEMO VIDEO
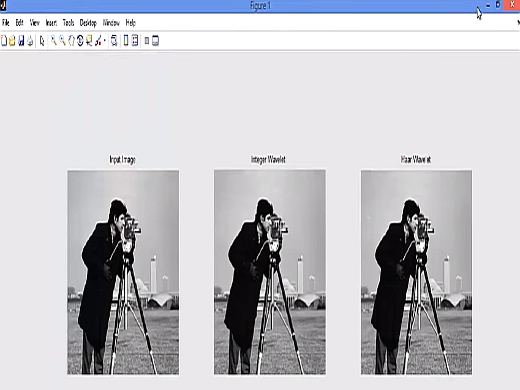
The problems of floating point precision of the wavelet filters is that when the input data is integer as in digital images, the output data will no longer be integer which doesn’t allow perfect reconstruction of the input image . Integer wavelet transform maps an integer data set into another integer data set. In IWT, there will be no loss of information through forward and inverse transform . In the case of IWT, the LL sub band appears to be a close copy of the original image, with smaller scale, while in the case of DWT; the resulting LL sub band is distorted. Lifting schemes is used to perform integer wavelet transform. Lifting consists of three stages: split, predict and update ]. The detailed steps are as follows.
Split: The data set Xi has some correlation structure and to obtain a more compact representation divide the original data set into odd subset {si0} and even subset {di0}.
Predict: Use the odd subset {sin-1} to predict even subset {din} based on the correlation present in the original data. Find a prediction operator P, independent of the data and predict sin-1, as given in (1).
The construction of a prediction operator P is typically based on some model of the data which reflects its correlation structure. If the prediction is reasonable, the subset will contain much less information than the original data set.
Update: Some global properties of the original data set in the subsets need to be maintained. This is performed by introducing update stage. The idea is to find a better sin. Construct an operator U and update sin as given in (2).
The forward update and prediction step is shown in Fig. 2.
Fig. 2. Forward update and prediction
The inverse transform involves the same steps as the forward transform, but they are applied in the reverse order and it has the same complexity. The introduction of decimal fraction mainly during the predicting and updating stage, make the factors become integer to achieve integer wavelet. The backward update and prediction step is shown in Fig. 3.
Fig. 3. Backward update and prediction
Integer wavelet based on lifting scheme has many merits such as high computational efficiency, less memory and accurate reconstruction [18].



Reviews
There are no reviews yet.