Description

What is K Means Algorithm

K-means  is one of the simplest unsupervised learning algorithms that solve the well known clustering problem. The procedure follows a simple and easy way to classify a given data set through a certain number of clusters (assume k clusters) fixed a priori. The main idea is to define k centroids, one for each cluster. These centroids shoud be placed in a cunning way because of different location causes different result. So, the better choice is to place them as much as possible far away from each other. The next step is to take each point belonging to a given data set and associate it to the nearest centroid. When no point is pending, the first step is completed and an early groupage is done. At this point we need to re-calculate k new centroids as barycenters of the clusters resulting from the previous step. After we have these k new centroids, a new binding has to be done between the same data set points and the nearest new centroid. A loop has been generated. As a result of this loop we may notice that the k centroids change their location step by step until no more changes are done.

Demonstration Videos

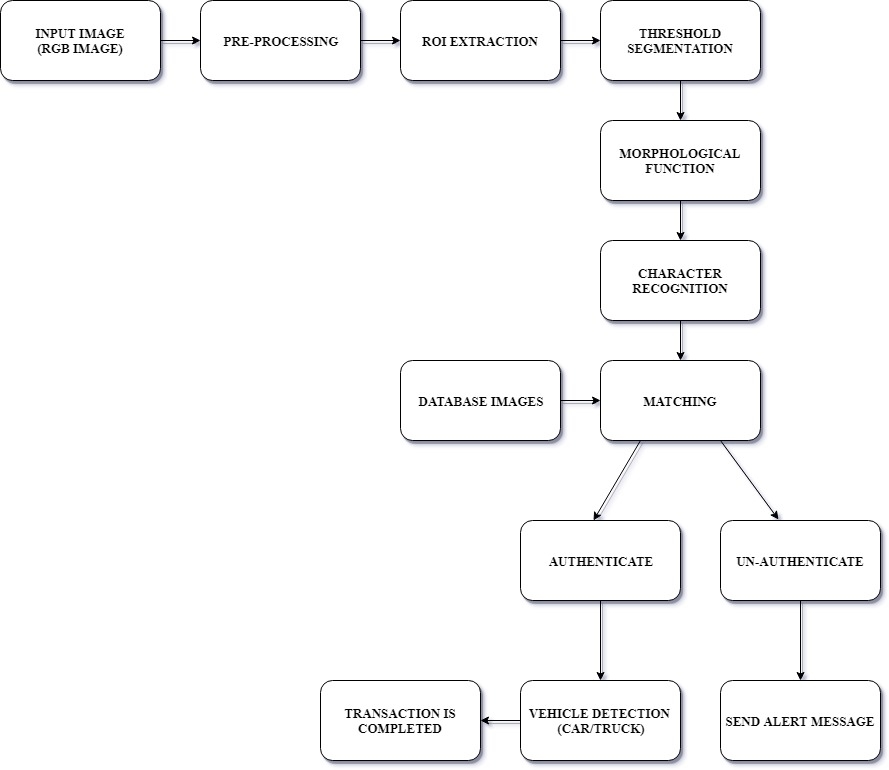
Algorithm for K Means Algorithm

1. Step 1:Read the image.

   Step 2:Get the number of clusters to be formed.

   Step 3:Convert the color image into its corresponding gray image.

   Step 4:Resize the two dimensional image into one dimensional array of length “r×c”.

   Step 5:Find the intensity range of the image.

                Range = [(Maximum intensity value)

                              – (Minimum intensity value)]

   Step 6:Find the centroid value

                Centroid 1 = Range/Number of clusters

                 Centroid 2 = (2 × Centroid 1)

   Step 7:Find the difference between the first intensity value and  the various centroid values.

   Step 8:Based on the minimum difference obtained, group the intensity  values into the corresponding clusters.

   Step 9:Repeat step 1 & 2 for all the other intensity values of the image.

           Centroid 3 = (3 × Centroid 1)

           Centroid  n = (n × Centroid 1)                            

                              

   

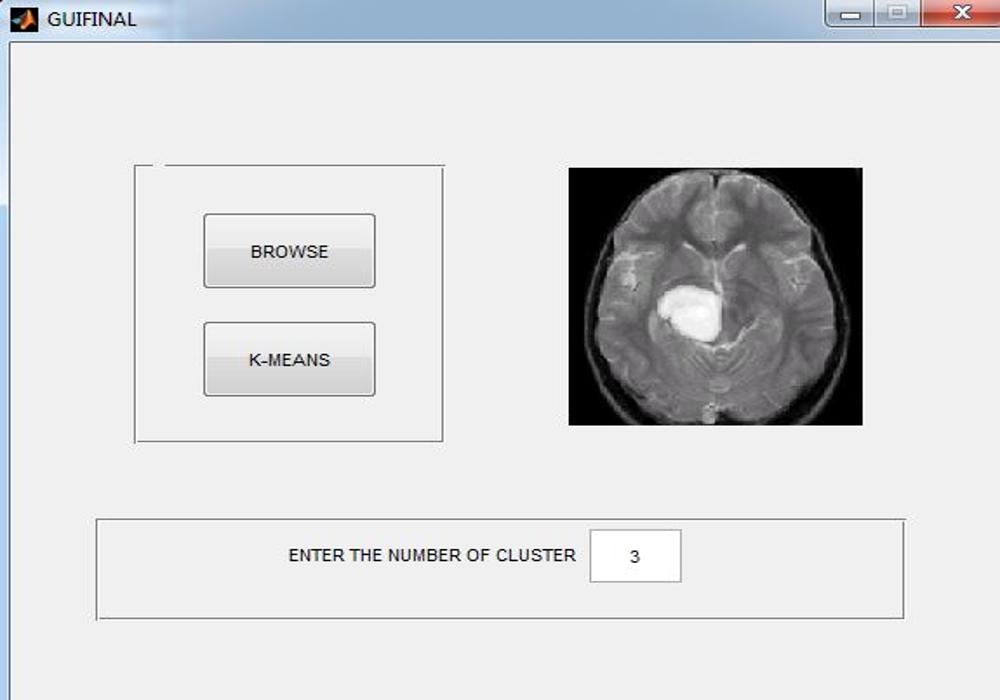
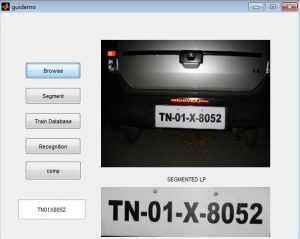
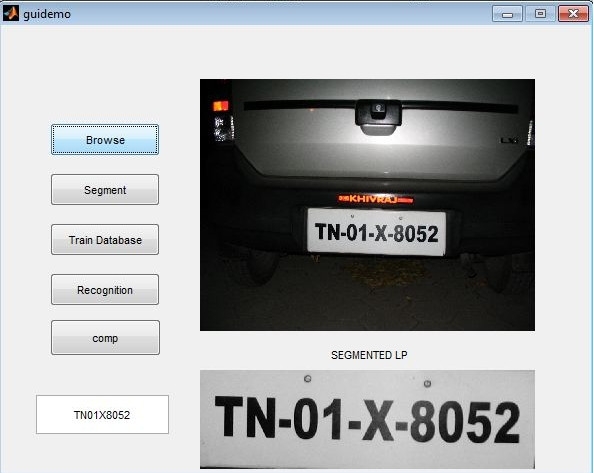
Matlab GUI for K means segmentation

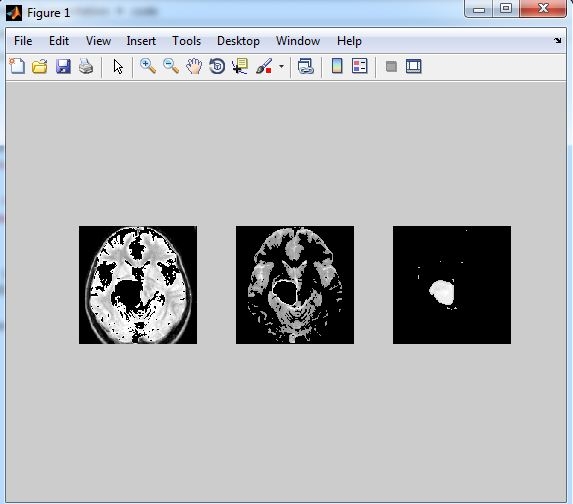
Result

Matlab Code for K Means Segmentation

function varargout = guifinal(varargin)

% GUIFINAL M-file for guifinal.fig
% GUIFINAL, by itself, creates a new GUIFINAL or raises the existing
% singleton*.
%
% H = GUIFINAL returns the handle to a new GUIFINAL or the handle to
% the existing singleton*.
%
% GUIFINAL(‘CALLBACK’,hObject,eventData,handles,…) calls the local
% function named CALLBACK in GUIFINAL.M with the given input arguments.
%
% GUIFINAL(‘Property’,’Value’,…) creates a new GUIFINAL or raises the
% existing singleton*. Starting from the left, property value pairs are
% applied to the GUI before guifinal_OpeningFunction gets called. An
% unrecognized property name or invalid value makes property application
% stop. All inputs are passed to guifinal_OpeningFcn via varargin.
%
% *See GUI Options on GUIDE’s Tools menu. Choose “GUI allows only one
% instance to run (singleton)”.
%
% See also: GUIDE, GUIDATA, GUIHANDLES

% Edit the above text to modify the response to help guifinal

% Last Modified by GUIDE v2.5 25-Sep-2006 12:53:17

% Begin initialization code – DO NOT EDIT
gui_Singleton = 1;
gui_State = struct(‘gui_Name’, mfilename, …
‘gui_Singleton’, gui_Singleton, …
‘gui_OpeningFcn’, @guifinal_OpeningFcn, …
‘gui_OutputFcn’, @guifinal_OutputFcn, …
‘gui_LayoutFcn’, [] , …
‘gui_Callback’, []);
if nargin & isstr(varargin{1})
gui_State.gui_Callback = str2func(varargin{1});
end

if nargout
[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:});
else
gui_mainfcn(gui_State, varargin{:});
end
% End initialization code – DO NOT EDIT

% — Executes just before guifinal is made visible.
function guifinal_OpeningFcn(hObject, eventdata, handles, varargin)
% This function has no output args, see OutputFcn.
% hObject handle to figure
% eventdata reserved – to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% varargin command line arguments to guifinal (see VARARGIN)

% Choose default command line output for guifinal
handles.output = hObject;

a=ones(256,256);
axes(handles.one);
imshow(a);

% Update handles structure
guidata(hObject, handles);

% UIWAIT makes guifinal wait for user response (see UIRESUME)
% uiwait(handles.figure1);

% — Outputs from this function are returned to the command line.
function varargout = guifinal_OutputFcn(hObject, eventdata, handles)
% varargout cell array for returning output args (see VARARGOUT);
% hObject handle to figure
% eventdata reserved – to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)

% Get default command line output from handles structure
varargout{1} = handles.output;

% — Executes on button press in Browse.
function Browse_Callback(hObject, eventdata, handles)
% hObject handle to Browse (see GCBO)
% eventdata reserved – to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)

[filename, pathname] = uigetfile(‘*.bmp’, ‘Pick an Image’);
if isequal(filename,0) | isequal(pathname,0)

warndlg(‘User pressed cancel’)

else

a=imread(filename);
axes(handles.one);
imshow(a);
handles.file=filename;
% Update handles structure
guidata(hObject, handles);
end

% — Executes on button press in pushbutton2.
function pushbutton2_Callback(hObject, eventdata, handles)
% hObject handle to pushbutton2 (see GCBO)
% eventdata reserved – to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)

bb=get(handles.e1,’String’);
bb=str2num(bb);
filename = handles.file;
if bb == 3
wd=256;
Input = imread(filename);
% imshow(Input);
figure;
Input =rgb2gray(Input);
Input =double(Input);
[r c] = size(Input);
Length = r*c;
Dataset = reshape(Input,[Length,1]);
Clusters=3 %k CLUSTERS
% Cluster1=[];
% Cluster2=[];
% Cluster3=[];
% Cluster4=[];
% Cluster5=[];
Cluster1=zeros(Length,1);
Cluster2=zeros(Length,1);
Cluster3=zeros(Length,1);
% Cluster4=zeros(Length,1);
% Cluster5=zeros(Length,1);

% Initial Centroids
% ARBITARLY CHOOSE K OBJECTS AS INITIAL CENTROIDS
miniv = min(min(Input));
maxiv = max(max(Input));
range = maxiv – miniv;
stepv = range/Clusters;
incrval = stepv;
for i = 1:Clusters
K(i).centroid = incrval;
incrval = incrval + stepv;
end

%BEGIN LOOP
% L=1;

update1=0;
update2=0;
update3=0;
update4=0;
update5=0;

mean1=2;
mean2=2;
mean3=2;
mean4=2;
mean5=2;

while ((mean1 ~= update1) & (mean2 ~= update2) & (mean3 ~= update3) )

mean1=K(1).centroid;
mean2=K(2).centroid;
mean3=K(3).centroid;
% mean4=K(4).centroid;
% mean5=K(5).centroid;

for i=1:Length
for j = 1:Clusters
temp= Dataset(i);
difference(j) = abs(temp-K(j).centroid);

end
[y,ind]=min(difference);

if ind==1
Cluster1(i) =temp;
end
if ind==2
Cluster2(i) =temp;
end
if ind==3
Cluster3(i) =temp;
end
% if ind==4
% Cluster4(i) =temp;
% end
% if ind==5
% Cluster5(i) =temp;
% end

end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%UPDATE CENTROIDS
cout1=0;
cout2=0;
cout3=0;
cout4=0;
cout5=0;

for i=1:Length
Load1=Cluster1(i);
Load2=Cluster2(i);
Load3=Cluster3(i);
% Load4=Cluster4(i);
% Load5=Cluster5(i);

if Load1 ~= 0
cout1=cout1+1;
end

if Load2 ~= 0
cout2=cout2+1;
end
%
if Load3 ~= 0
cout3=cout3+1;
end

% if Load4 ~= 0
% cout4=cout4+1;
% end
%
% if Load5 ~= 0
% cout5=cout5+1;
% end
end

% find the new mean of centroids

% Mean_Cluster(1)=sum(Cluster1)/Length;
% Mean_Cluster(2)=sum(Cluster2)/Length;
% Mean_Cluster(3)=sum(Cluster3)/Length;
% Mean_Cluster(4)=sum(Cluster4)/Length;
% Mean_Cluster(5)=sum(Cluster5)/Length;

Mean_Cluster(1)=sum(Cluster1)/cout1;
Mean_Cluster(2)=sum(Cluster2)/cout2;
Mean_Cluster(3)=sum(Cluster3)/cout3;
% Mean_Cluster(4)=sum(Cluster4)/cout4;
% Mean_Cluster(5)=sum(Cluster5)/cout5;
%reload
for i = 1:Clusters
K(i).centroid = Mean_Cluster(i);

end

update1=K(1).centroid;
update2=K(2).centroid;
update3=K(3).centroid;
% update4=K(4).centroid;
% update5=K(5).centroid;

end

AA1=reshape(Cluster1,[wd wd]);
AA2=reshape(Cluster2,[wd wd]);
AA3=reshape(Cluster3,[wd wd]);
% AA4=reshape(Cluster4,[wd wd]);
% AA5=reshape(Cluster5,[wd wd]);
subplot(1,3,1);imshow(AA1,[]);
%figure;
subplot(1,3,2);imshow(AA2,[]);
%figure;
subplot(1,3,3);imshow(AA3,[]);
% figure;
% imshow(AA4,[]);
% figure;
% imshow(AA5,[]);

elseif bb == 4
wd=256;
Input = imread(filename);
imshow(Input);
figure;
Input =rgb2gray(Input);
Input =double(Input);
[r c] = size(Input);
Length = r*c;
Dataset = reshape(Input,[Length,1]);
Clusters=4 %k CLUSTERS
% Cluster1=[];
% Cluster2=[];
% Cluster3=[];
% Cluster4=[];
% Cluster5=[];
Cluster1=zeros(Length,1);
Cluster2=zeros(Length,1);
Cluster3=zeros(Length,1);
Cluster4=zeros(Length,1);
% Cluster5=zeros(Length,1);

% Initial Centroids
% ARBITARLY CHOOSE K OBJECTS AS INITIAL CENTROIDS
miniv = min(min(Input));
maxiv = max(max(Input));
range = maxiv – miniv;
stepv = range/Clusters;
incrval = stepv;
for i = 1:Clusters
K(i).centroid = incrval;
incrval = incrval + stepv;
end

%BEGIN LOOP
% L=1;

update1=0;
update2=0;
update3=0;
update4=0;
update5=0;

mean1=2;
mean2=2;
mean3=2;
mean4=2;
mean5=2;

while ((mean1 ~= update1) & (mean2 ~= update2) & (mean3 ~= update3) & (mean4 ~= update4))

mean1=K(1).centroid;
mean2=K(2).centroid;
mean3=K(3).centroid;
mean4=K(4).centroid;
% mean5=K(5).centroid;

for i=1:Length
for j = 1:Clusters
temp= Dataset(i);
difference(j) = abs(temp-K(j).centroid);

end
[y,ind]=min(difference);

if ind==1
Cluster1(i) =temp;
end
if ind==2
Cluster2(i) =temp;
end
if ind==3
Cluster3(i) =temp;
end
if ind==4
Cluster4(i) =temp;
end
% if ind==5
% Cluster5(i) =temp;
% end

end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%UPDATE CENTROIDS
cout1=0;
cout2=0;
cout3=0;
cout4=0;
cout5=0;

for i=1:Length
Load1=Cluster1(i);
Load2=Cluster2(i);
Load3=Cluster3(i);
Load4=Cluster4(i);
% Load5=Cluster5(i);

if Load1 ~= 0
cout1=cout1+1;
end

if Load2 ~= 0
cout2=cout2+1;
end
%
if Load3 ~= 0
cout3=cout3+1;
end

if Load4 ~= 0
cout4=cout4+1;
end
%
% if Load5 ~= 0
% cout5=cout5+1;
% end
end

% find the new mean of centroids

% Mean_Cluster(1)=sum(Cluster1)/Length;
% Mean_Cluster(2)=sum(Cluster2)/Length;
% Mean_Cluster(3)=sum(Cluster3)/Length;
% Mean_Cluster(4)=sum(Cluster4)/Length;
% Mean_Cluster(5)=sum(Cluster5)/Length;

Mean_Cluster(1)=sum(Cluster1)/cout1;
Mean_Cluster(2)=sum(Cluster2)/cout2;
Mean_Cluster(3)=sum(Cluster3)/cout3;
Mean_Cluster(4)=sum(Cluster4)/cout4;
% Mean_Cluster(5)=sum(Cluster5)/cout5;
%reload
for i = 1:Clusters
K(i).centroid = Mean_Cluster(i);

end

update1=K(1).centroid;
update2=K(2).centroid;
update3=K(3).centroid;
update4=K(4).centroid;
% update5=K(5).centroid;

end

AA1=reshape(Cluster1,[wd wd]);
AA2=reshape(Cluster2,[wd wd]);
AA3=reshape(Cluster3,[wd wd]);
AA4=reshape(Cluster4,[wd wd]);
% AA5=reshape(Cluster5,[wd wd]);
subplot(2,2,1);imshow(AA1,[]);
%figure;
subplot(2,2,2);imshow(AA2,[]);
%figure;
subplot(2,2,3);imshow(AA3,[]);
%figure;
subplot(2,2,4);imshow(AA4,[]);
% figure;
% imshow(AA5,[]);

elseif bb== 5
% % number of clusters k and dataset containing n objects
% clc;
% clear;
% close all;
wd=256;
Input = imread(filename);
% imshow(Input);
figure;
Input =rgb2gray(Input);
Input =double(Input);
[r c] = size(Input);
Length = r*c;
Dataset = reshape(Input,[Length,1]);
Clusters=5 %k CLUSTERS
% Cluster1=[];
% Cluster2=[];
% Cluster3=[];
% Cluster4=[];
% Cluster5=[];
Cluster1=zeros(Length,1);
Cluster2=zeros(Length,1);
Cluster3=zeros(Length,1);
Cluster4=zeros(Length,1);
Cluster5=zeros(Length,1);

% Initial Centroids
% ARBITARLY CHOOSE K OBJECTS AS INITIAL CENTROIDS
miniv = min(min(Input));
maxiv = max(max(Input));
range = maxiv – miniv;
stepv = range/Clusters;
incrval = stepv;
for i = 1:Clusters
K(i).centroid = incrval;
incrval = incrval + stepv;
end

%BEGIN LOOP
% L=1;

update1=0;
update2=0;
update3=0;
update4=0;
update5=0;

mean1=2;
mean2=2;
mean3=2;
mean4=2;
mean5=2;

while ((mean1 ~= update1) & (mean2 ~= update2) & (mean3 ~= update3) & (mean4 ~= update4) & (mean5 ~= update5))

mean1=K(1).centroid;
mean2=K(2).centroid;
mean3=K(3).centroid;
mean4=K(4).centroid;
mean5=K(5).centroid;

for i=1:Length
for j = 1:Clusters
temp= Dataset(i);
difference(j) = abs(temp-K(j).centroid);

end
[y,ind]=min(difference);

if ind==1
Cluster1(i) =temp;
end
if ind==2
Cluster2(i) =temp;
end
if ind==3
Cluster3(i) =temp;
end
if ind==4
Cluster4(i) =temp;
end
if ind==5
Cluster5(i) =temp;
end

end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%UPDATE CENTROIDS
cout1=0;
cout2=0;
cout3=0;
cout4=0;
cout5=0;

for i=1:Length
Load1=Cluster1(i);
Load2=Cluster2(i);
Load3=Cluster3(i);
Load4=Cluster4(i);
Load5=Cluster5(i);

if Load1 ~= 0
cout1=cout1+1;
end

if Load2 ~= 0
cout2=cout2+1;
end
%
if Load3 ~= 0
cout3=cout3+1;
end

if Load4 ~= 0
cout4=cout4+1;
end

if Load5 ~= 0
cout5=cout5+1;
end
end

% find the new mean of centroids

% Mean_Cluster(1)=sum(Cluster1)/Length;
% Mean_Cluster(2)=sum(Cluster2)/Length;
% Mean_Cluster(3)=sum(Cluster3)/Length;
% Mean_Cluster(4)=sum(Cluster4)/Length;
% Mean_Cluster(5)=sum(Cluster5)/Length;

Mean_Cluster(1)=sum(Cluster1)/cout1;
Mean_Cluster(2)=sum(Cluster2)/cout2;
Mean_Cluster(3)=sum(Cluster3)/cout3;
Mean_Cluster(4)=sum(Cluster4)/cout4;
Mean_Cluster(5)=sum(Cluster5)/cout5;
%reload
for i = 1:Clusters
K(i).centroid = Mean_Cluster(i);

end

update1=K(1).centroid;
update2=K(2).centroid;
update3=K(3).centroid;
update4=K(4).centroid;
update5=K(5).centroid;

end

AA1=reshape(Cluster1,[wd wd]);
AA2=reshape(Cluster2,[wd wd]);
AA3=reshape(Cluster3,[wd wd]);
AA4=reshape(Cluster4,[wd wd]);
AA5=reshape(Cluster5,[wd wd]);
subplot(3,2,1);imshow(AA1,[]);
% figure;
subplot(3,2,2);imshow(AA2,[]);
% figure;
subplot(3,2,3);imshow(AA3,[]);
% figure;
subplot(3,2,4);imshow(AA4,[]);
% figure;
subplot(3,2,5);imshow(AA5,[]);

else

helpdlg(‘The no of cluster should be 3,4 or 5’);

end

%

function e1_Callback(hObject, eventdata, handles)
% hObject handle to e1 (see GCBO)
% eventdata reserved – to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)

% Hints: get(hObject,’String’) returns contents of e1 as text
% str2double(get(hObject,’String’)) returns contents of e1 as a double