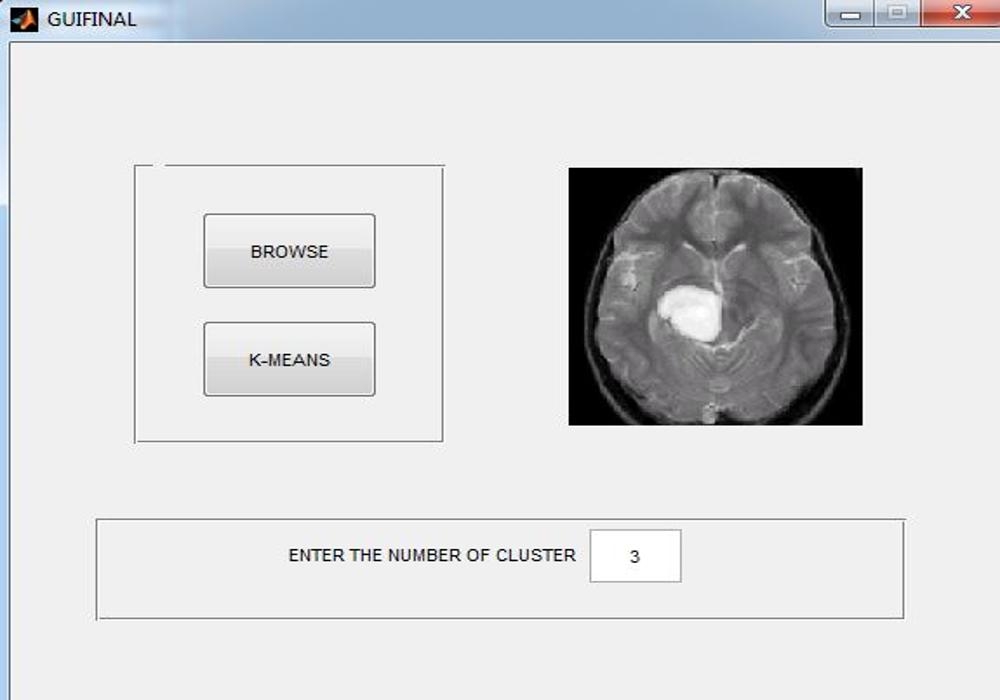
Matlab code for Detection of Microcalcification
₹3,000.00
Huge Price Drop : 50% Discount
Source Code + Demo Video
100 in stock
Description
ABSTRACT
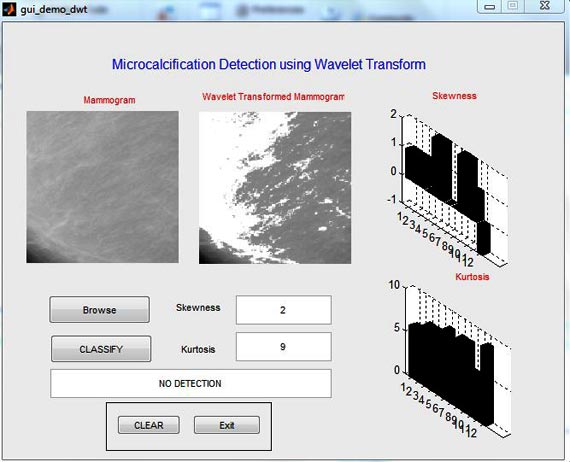
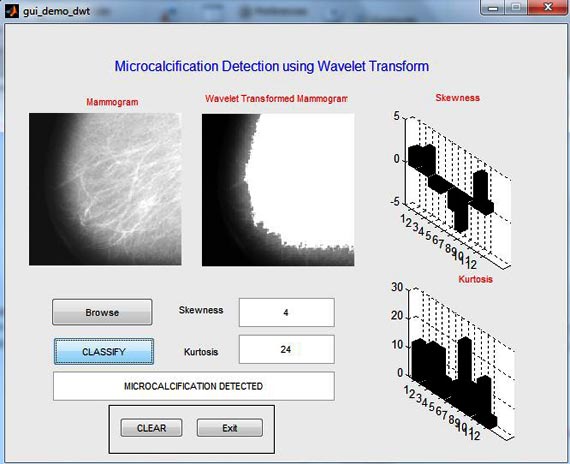
Mammography is the most efficient modality for detection of breast cancer at early stage. Microcalcifications are tiny bright spots in mammograms and can often get missed by the radiologist during diagnosis. The presence of microcalcification clusters in mammograms can act as an early sign of breast cancer. This paper presents a completely region of interest(ROI) system for detection of microcalcification clusters in mammograms. Blurry masking is used as a preprocessing step which enhances the contrast between microcalcifications and the background. The preprocessed image is threshold and various shape and intensity based features are extracted. Neural Networks(NN) classifier is used to reduce the false positives while preserving the true microcalcification clusters
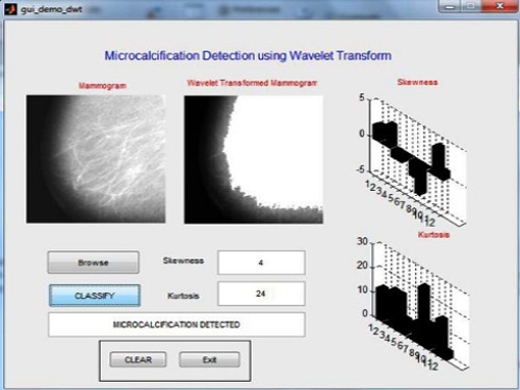
DEMO VIDEO
INTRODUCTION
Breast cancer is one of the leading causes of cancer-related deaths. early detection of suspicious lesions is crucial for the prognosis of the patient. In cases where a lesion is detected before cancer cells spread into the surrounding tissue, the 5-year survival rate is 97.9%. It drops sharply to 81.3% and 26.1% for regionally advanced and metastatic cancer, respectively Detection of breast cancer is conducted by means of two most widely used diagnostic methods, i.e., mammography and ultrasonography (USG) imaging. These two methods are best suited for unveiling different types of cancer . The system processes the mammograms in several steps. First, we filter the original picture with a filter that is sensitive to microcalcification contrast shape. Then, we enhance the mammogram contrast by using wavelet-based sharpening algorithm. Afterwards, we present to radiologist, for visual analysis, such a contrast-enhanced mammogram with suggested positions of microcalcification clusters. We have evaluated the usefulness of the system with the help of four experienced radiologists, who found that it significantly improves the detection of microcalcifications in small field digital mammography.
EXISTING SYSTEM
In existing system we used DCT(discrete cosine transform) technique and SVM(support vector machine) algorithm. Here DCT will be used for segmentation process of micro parts in image. After the segmentation process we will go to the classification using support vector machine. But in this system we cant get the accurate counts of micro particles of query image, so we are proposing a new technique to accurate the results.
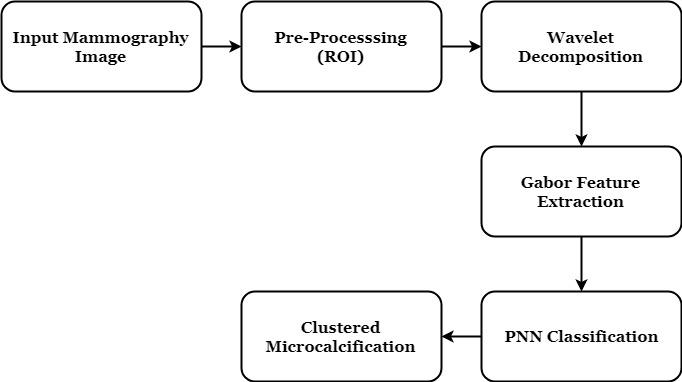
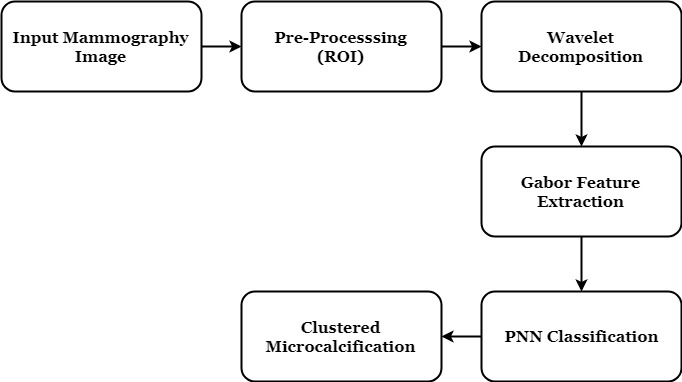
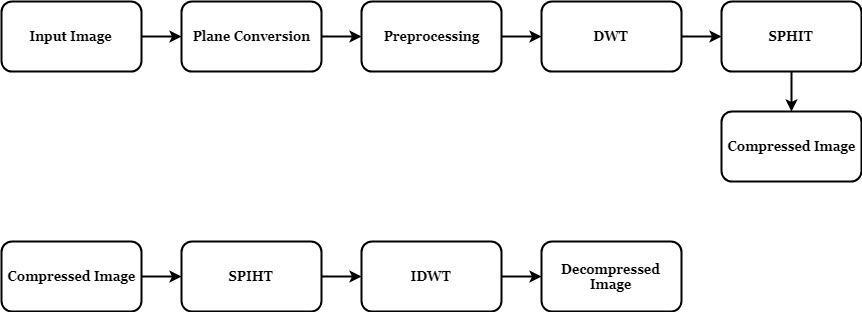
PROPOSED METHOD
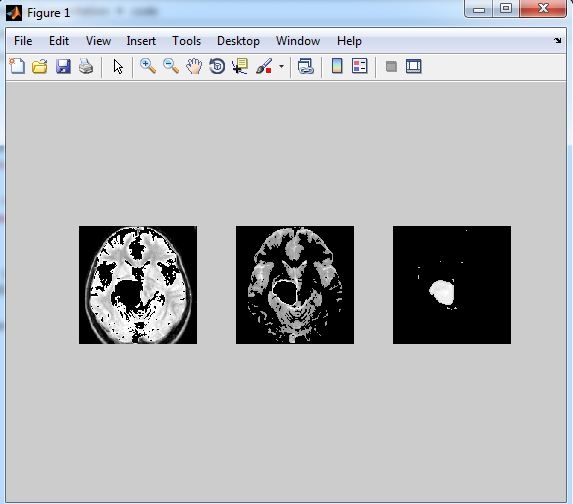
The proposed microcalcification detection method is done in two stages. In the first stage, features are extracted to discriminate between textures representing clusters of microcalcifications and texture representing normal tissue. The original mammogram image is decomposed using wavelet decomposition and Gabor features are extracted from the original image Region of Interest (ROI). With these features individual microcalcification clusters is detected. In the second stage, the ability of these features in detecting microcalcification is done using Probability Neural Network (PNN).
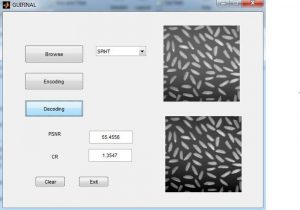
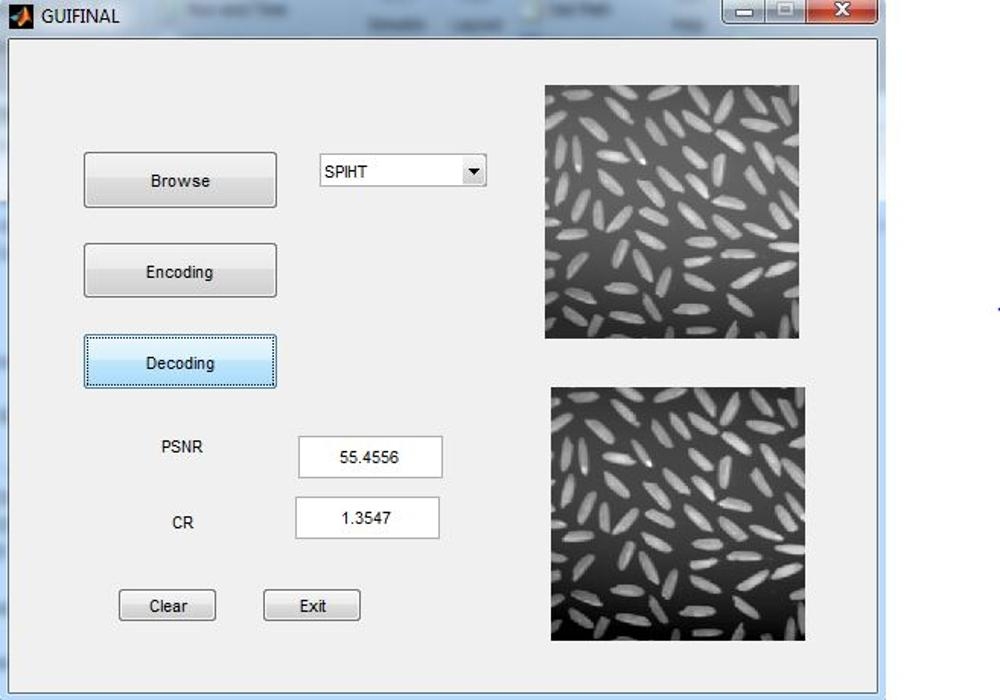
BLOCK DIAGRAM
ADVANTAGES
- Estimating exact features using Gabor feature extraction
- Improvement in data set images training
APPLICATIONS
- Medical applications
- Small particles classifications
SOFTWARE REQUIREMENTS
- MATLAB 7.14 or above versions
Matlab code for micro calcification detection
CONCLUSION
The algorithm developed here classifies mammograms into normal & abnormal. First, the structures in mammograms produced by normal glandular tissue of varying density are eliminated using a Integer Wavelet Transform (IWT) based local average subtraction. The Gabor features are extracted and classification approaches using artificial neural networks shows good classification results. Using the mammographic data from the Mammographic Image Analysis Society (MIAS) database a recognition score of 84.3% was achieved using the proposed approach.
REFERENCES
[1] Pisani et al. “Outcome of screening by Clinical Examination of the Breast in a Trial in the Phillipines”. Int. J. Cancer, 2006.
[2] L.Shen, R.M. Rangaan, and J.E.L. Desautels, “Application of shape analysis to mammographic classifications,” IEEE Trans. Med. Imag., vol, 13, no. 2, pp. 263-24, Jun, 1994.
[3] S.K.Lee, P.Chung, C.L.Chang, C.S. Lo, T.Lee, G.C. Hsu, and C.W. ang, “Classification of Clustered Microcalcifications using shape cognitron neural network,” Neural Netw., vol.16, no. 1, pp. 121-132, Jan. 2003.
[4] A.P. Dhawan, . Chitre, C. Kaiser-Bonasso, and M. Moskoitz, Analysis of mammographic microcalcification using gray-level image structure features,“ IEEE Trans. Med. Imag., vol.15, no. 3, pp. 11-150, Jun. 2005.
[5] Joaquim.C. Felipe et al. “Effective shape based retrival and classification of mammograms,” Proceeding of the ACM Smposium in Applied Computing, 2006.
[6] Chen. And Chang.C “New Texture shape feature coding based computer aided diagnostic methods for classification of masses on mammograms,” Engg. In Medicine and Biology Society IEMBS 26th Annual Int. Conference of the IEEE, vol. 1, pp. 1275-128, 2004.
[7] A. M. Khuzi, R. Besar and .M.D. an Zaki, “Texture feature selection for masses detection in digital mammograms,” IFMBE Proceedings springerlink, vol. 21, pp. 629-632.
[8] Pelin Gorgel, Ahmet serlbas et al. “mammogram mass classification using wavelet based support vector machine,” Journal of Electrical and Electronics Engg, vol.9, no.1, pp. 86-875, 2009.




Reviews
There are no reviews yet.